Test je wiskundige capaciteiten!

Test je wiskundige capaciteiten en probeer één of meer van de onderstaande problemen op te lossen.

Hieronder staan opgaves zoals je die tijdens de verschillende rondes van de Nederlandse Wiskunde Olympiade (NWO) zou kunnen tegenkomen. De 'eenvoudigste' opgaven moeten door 2 vwo scholieren gemaakt kunnen worden.

Bij deze serie oudere opgaven hebben we ook de bijbehorende uitwerkingen toegevoegd. Niet meteen spieken!

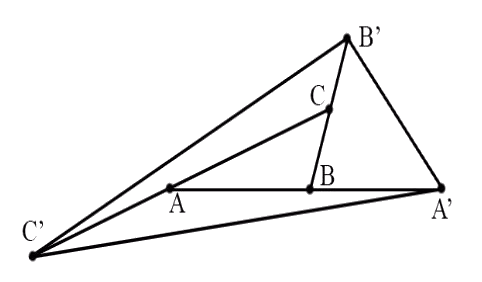
De driehoek ABC heeft een oppervlakte 5.

We puntspiegelen A in B, dat geeft punt A’.

We puntspiegelen B in C, dat geeft punt B’.

En we puntspiegelen C in A, dat geeft punt C’.

➢ Bereken de oppervlakte van driehoek A’B’C’.

A is het grote getal van 8068 cijfers dat ontstaat door 2017 maal het getal 2017 achter elkaar te zetten, dus A = 201720172017⋯

B = A² − 1

➢ Is B deelbaar door 144?

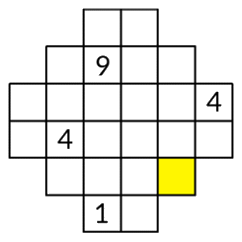
Leanne vult de afgebeelde tabel volledig met getallen. Daarbij gelden de volgende regels:

• Van elk drietal getallen dat naast elkaar staat is het middelste getal het gemiddelde van de getallen links en rechts.
  
• Van elk drietal getallen dat boven elkaar staat is het middelste getal het gemiddelde van de getallen boven en onder.
  
  

➢ Welk getal zet Leanne in het gele hokje?

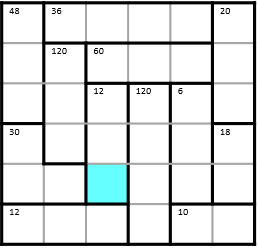
Plaats in het afgebeelde raster in elke rij en in elke kolom de cijfers 1 t/m 6 elk eenmaal, zodanig dat het product van de cijfers in elk van de 12 aangeduide blokken gelijk is aan het getal dat links bovenin elk blok staat. In eenzelfde blok mag niet tweemaal hetzelfde cijfer komen te staan.

➢ Welk cijfer komt er in het blauwe hokje te staan?

Bastiaan gaat altijd op de fiets naar school. Hij kan ook gaan lopen, maar dan doet hij er precies driemaal zo lang over. Op een regenachtige dag krijgt Bastiaan onderweg naar school een lekke band. Hij kan nu 3 dingen doen:

• Doorlopen naar school.
• Teruglopen naar huis en dan met de fiets van zijn vader naar school.
• De band plakken (dat duurt 20 minuten) en dan doorfietsen naar school.

Bastiaan slaat even aan het rekenen en ontdekt dat alle drie de keuzes precies even lang duren.

➢ Hoe lang duurt de fietstocht van huis naar school als hij geen lekke band heeft?

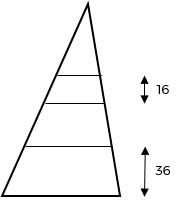
Een driehoek wordt opgebouwd uit gestapelde gelijkvormige trapezia (zie schets). Het onderste trapezium heeft een hoogte 36. De derde van onder heeft een hoogte 16.

➢ Bereken de hoogte van de driehoek.

We noemen een getal oplopend wanneer elk cijfer van het getal groter is dan het cijfer dat er (eventueel) voor staat. Dus de getallen 38 en 237 zijn oplopend, maar bijvoorbeeld ook het getal 8.

➢ Hoeveel van de getallen 1 t/m 1000 zijn oplopend?

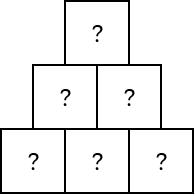
De hier afgebeelde piramide moet met 6 verschillende positieve gehele getallen worden gevuld. Op elk van de stenen moet een getal komen te staan, zodanig dat de som van de getallen op de onderste rij gelijk is aan de som van de getallen in de tweede rij, en gelijk is aan het getal op de bovenste steen.

➢ Bepaal het kleinst mogelijke getal op de bovenste steen.

M=123456……999 is het hele grote getal dat ontstaat door alle getallen 1 t/m 999 achter elkaar te zetten.

➢ Als we M delen door 9, welke rest houden we dan over?

Als de schets hiernaast netjes op schaal was geweest, dan had je een rechthoek gezien die is opgedeeld in 6 vierkantjes. De oppervlakte van het kleinste vierkant is 1.

➢ Bereken de oppervlakte van de volledige rechthoek.