Opgave 1
De driehoek ABC heeft een oppervlakte 5.
We puntspiegelen A in B, dat geeft punt A’.
We puntspiegelen B in C, dat geeft punt B’.
En we puntspiegelen C in A, dat geeft punt C’.
➢ Bereken de oppervlakte van driehoek A’B’C’.
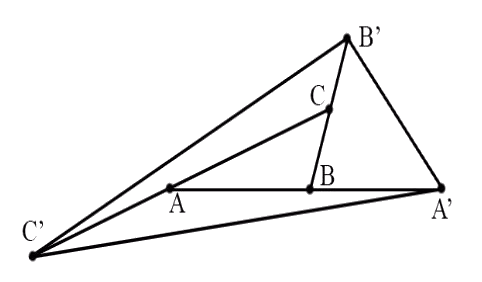
Uitwerking
De oppervlakte van een driehoek wordt gegeven door ½ ∙ hoogte ∙ basis. Dan zien we dat de oppervlakte van driehoek BA’B’ twee keer zo groot is als die van driehoek ABC. Immers, als we voor deze driehoeken respectievelijk BA’ en AB nemen als basis, dan zien we dat de basis van deze twee driehoeken gelijk is. Terwijl de hoogte van BA’B’ twee keer zo groot is als de hoogte van ABC (want C ligt precies op het midden van BB’).
Op dezelfde wijze kunnen we beredeneren dat de oppervlakten van de driehoeken CB’C’ en AC’A’ beide ook twee keer zo groot zijn als de oppervlakte van ABC.
Tot slot weten we ook nog dat de oppervlakte van A’B’C’ gelijk is aan de som van de oppervlakten van de vier driehoeken ABC, BA’B’, CB’C’ en AC’A’. En dat de oppervlakte van driehoek ABC gelijk is aan 5.
Dus de oppervlakte van driehoek A’B’C’ is gelijk aan: (1 + 2 + 2 + 2) ∙ 5 = 7 ∙ 5 = 35.