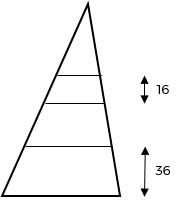
Een driehoek wordt opgebouwd uit gestapelde gelijkvormige trapezia (zie schets). Het onderste trapezium heeft een hoogte 36. De derde van onder heeft een hoogte 16.

➢ Bereken de hoogte van de driehoek.

De gezochte hoogte van de driehoek noemen we h. We noemen de breedte van de basis van de driehoek en het onderste trapezium b. En we stellen dat de breedte van de bovenkant van het onderste trapezium daar een fractie f van is.

Daaruit volgt de hoogte van de driehoek die daar bovenop staat f ∙ h is. Dus de hoogte van het onderste trapezium is (1 – f) ∙ h. Gegeven is dat die hoogte gelijk is aan 36. Dus:

(1 – f) ∙ h = 36 ⇔ h = 36 / (1 – f)

Nu hoeven we alleen f nog maar te berekenen. Alle trapezia zijn gelijkvormig. Dus voor allemaal moet gelden dat de lengte van de bovenste zijde gelijk is aan f maal de lengte van de onderste zijde. Daaruit volgt dat de lengte van de basis van het derde trapezium gelijk is aan f² maal de lengte van de basis van het onderste trapezium. Wegens de gelijkvormigheid volgt daaruit dat ook de hoogte van het derde trapezium gelijk is aan f² maal de hoogte van het onderste trapezium. Invullen geeft:

f² ∙ 36 = 16 ⇔ f² = 16 / 36 ⇔ f = 4 / 6 = 2 / 3

Als we dit invullen in de al gevonden formule voor de hoogte, dan krijgen we:

h = 36 / (1 – f) = 36 / (1 / 3) = 108