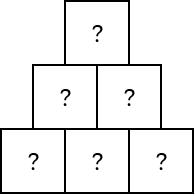
De hier afgebeelde piramide moet met 6 verschillende positieve gehele getallen worden gevuld. Op elk van de stenen moet een getal komen te staan, zodanig dat de som van de getallen op de onderste rij gelijk is aan de som van de getallen in de tweede rij, en gelijk is aan het getal op de bovenste steen.

➢ Bepaal het kleinst mogelijke getal op de bovenste steen.

Als in de onderste 2 rijen de 5 kleinste positieve gehele getallen staan, dus 1 t/m 5, dan tellen die op tot 15. Omdat de som van de getallen in de onderste rij gelijk is aan de som van de getallen in de tweede rij, moet dat bij elkaar een even getal geven. Dat geeft als kleinste mogelijkheid 16, met een som 8 in elke rij. Dat kan alleen met de getallen 1, 2, 3, 4, en 6. En dat lukt met de getallen 1, 3 en 4 in de onderste rij en de getallen 2 en 6 in de tweede rij.