One day the thermometer reads 10 ⁰C; the next day 15 ⁰C. Did it get 50% warmer? Measured in Fahrenheit, we would have seen only an 18% rise, from 50 ⁰F to 59 ⁰F. And in Kelvin only a 1.8% rise. Celsius and Kelvin essentially use the same scale. The only difference is the position of zero. With Celsius this is the level below which water freezes, whereas 0 Kelvin refers to an absolute zero.

In the history of mathematics, the invention of zero in the 7th century by the Indian mathematician and astronomer Brahmagupta marked a real breakthrough. From that moment onwards ‘nothing’ became an important pivot point in many calculations. Also, the concept of relative measures is based on the existence and relevance of zero. ‘Twice as large’ as a measure essentially means ‘at twice the distance from zero’. Eight is twice as large as four, measured from nil. However, eight is five time as large as four when measured from three. An important consequence is that the meaningfulness of relative measures is completely determined by the relevance of the defined zero.

In finance, many people are addicted to the use of relative measures. Price changes are usually expressed in relative numbers – a stock rises or falls by 2%, and so forth. To some extent, this habit is indisputable. If coffee rises from 120 cents per pound to 126 cents, this represents the exact same rise as from $2,645.5 per tonne to $2,777.8. But is this comparable to a price rise of Starbucks stocks from $80 to $84?

The position of zero seems to be indisputable in finance. At a price of zero you can get the stuff for free. At a price above zero you have to pay for it. But this is only from the buyer’s perspective. For the coffee producer, for instance, the meter only starts running after production costs have been covered. Prices below that level represent negative territory.

Negative prices do not fit this relative price framework. In models constructed around relative returns, prices can decline indefinitely but never end up below zero. After three consecutive 50% declines, a good still holds 1/8th of its value. However, in the real economy prices of goods and services do occasionally reach negative levels. Last April this happened in the May ’20 futures contract of WTI Crude Oil, on the day before its final trading day.

Negative prices: May ’20 futures contract of WTI Crude Oil

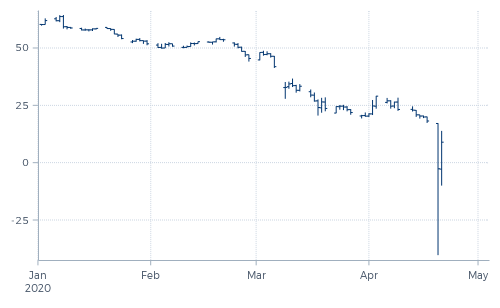
This might have been unprecedented in oil futures, but surely not in other areas of the economy. By now, most of you will be familiar with paying (negative) interest rates on funds deposited at banks. Also, negative prices for physical commodities have been a recurring phenomenon for many years. This happens for instance when producers have to pay for (or otherwise incur costs to get rid of) products that no one is willing or able to buy. We regularly see this in the European power market during off-peak hours, when production is higher than the immediate demand. It also occasionally happens in agricultural commodities such as livestock and dairy, for instance when farmers produce more milk than they are allowed to deliver to their dairy cooperatives.

Part of the reason for using zero as the ultimate floor for commodity prices was the idea that producers can just get rid of their excess production if they don’t get paid, sometimes literally by flushing it down the drain. But due to the growing awareness of pollution, this isn’t always possible anymore. In Europe, for instance, legislation has made it harder for producers to flare gas at oil production sites. As such, we could say that putting a price tag on pollution has broken the ice floor of zero. And perhaps this development will at some point extend beyond the perishable commodities. For instance to infrastructure: what is the price of a closed-down bridge across a river? Whether this could also apply to stocks is essentially determined by legal definitions rather than by economic reality. To what extent can owners of a company be held liable for remaining damages after the company goes bankrupt?

We can conclude that the zero in finance is comparable to the zero on the Celsius temperature scale. It might have a clear fundamental meaning, but it isn’t as low as it can get. In itself this is not a problem. It just implies that all models using relative price changes have to be adapted, allowing for a more sustainable absolute zero.